Daily Dose of DSA - Day 3
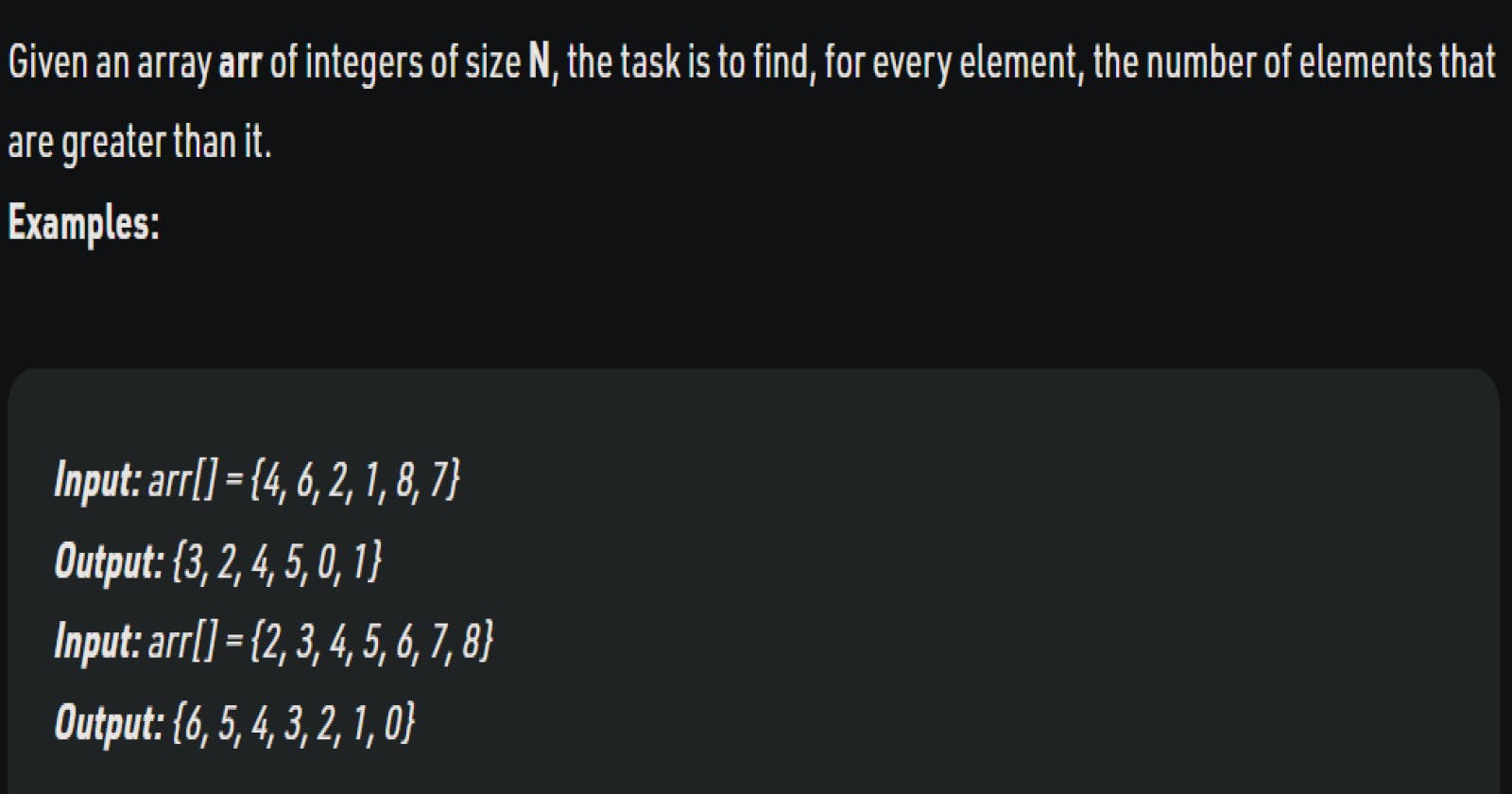
Number of greater elements for every array element using naive method (θ(n²)) , tree map (O(nlogn)) and upper bound method(O(nlogn))
Table of contents
No headings in the article.
void printgreater(int arr[], int n) // naive approach θ(n²)
{
for (int i = 0; i < n; i++) // traverse the array
{
int count = 0;
for (int j = 0; j < n; j++)
if (j != i && arr[j] > arr[i])
count++; // for every greater element found , increment the count
cout << count << " ";
}
}
void Printgreater(int arr[], int n) // efficient way O(nlogn)
{
map<int, int> m; // map O(n) auxiliary space
for (int i = 0; i < n; i++)
m[arr[i]]++; // Traverse the array, map the key & value
int cum_freq = 0; // cumulative freq
/*this cumulative frequency will hold
the values of the number of greater elements */
for (auto it = m.rbegin(); it != m.rend(); it++) // iterating through the map
{
int freq = it->second; // value stored to freq
it->second = cum_freq; // cum.freq assigned to it.second of map
cum_freq += freq; // cum.freq incremented by the stored value
}
for (int i = 0; i < n; i++)
cout << m[arr[i]] << " "; // print the cum.freq according to array elements
}
void PrintGreater(int arr[], int n) //efficient way O(nlogn)
{
vector<int> temp(n); //vector ini
for (int i = 0; i < n; i++)
{
temp[i] = arr[i]; //copy in temp
}
sort(temp.begin(), temp.end()); //sort the temp
for (int i = 0; i < n; i++)
{
auto it = upper_bound(temp.begin(), temp.end(), arr[i]); // iterator to upper bound of the ith element in sorted vector
auto it1 = temp.end() - 1; //iterator to the end of the sorted vector
if (it != temp.end()) //if upper bound is present
cout << it1 - it + 1 /*binary_search(temp.begin(), temp.end(), *it)*/ << " ";
else
cout << 0 << " "; //if upper bound is not present
}
}
int main()
{
int arr[] = {10, 2, 8, 5, 8}, n = 4;
printgreater(arr, n); //θ(n²) TC
Printgreater(arr,n); // O(nlogn) TC , O(n) AS
PrintGreater(arr,n); // O(nlogn) TC , O(n) AS
}